EJERCICIO DE CONVEXIDAD DE FUNCIONES.

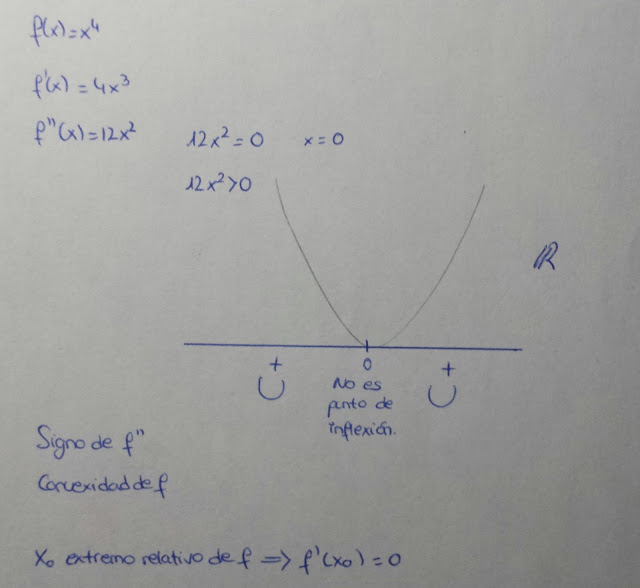
PROPOSICIÓN:

PROPOSICIÓN 2:

PROBLEMAS DE OPTIMIZACIÓN: 
Encontrar los extremos absolutos de una función continua y derivable (a veces no) restringida a un intervalo.

Procedimiento para encontrar los extremos absolutos:

1.Encontrar los extremos relativos (a partir de la derivada f')

2. En los extremos relativos encontrados, evaluar la función f para compararlos.

EJERCICIO:

ESTUDIO COMPLETO DE UNA FUNCIÓN (2)

1. Dominio
2. Cortes con los ejes (ceros de f; con el eje x).
3. Continuidad y asíntotas (verticales, horizontales y oblicuas).
4. Monotonía y extremos relativos de f (f').
5. Convexidad y puntos de inflexión.
6. Gráfica de f.

ESTUDIO COMPLETO DE UNA FUNCIÓN.

1. Dominio
2. Simetría
3. Periocidad
4. Punto de corte con los ejes 
5. Signo de la función
6. Asíntotas
7. Crecimiento y decrecimiento
8. Máximos y mínimos
9. Concavidad y convexidad. Puntos de inflexión
10. Gráfica

APLICACIONES DE LA DERIVADA.

• Relación entre: monotonía y extremos relativos de una función, y signo y ceros de la función derivada.
• Proposición:

EJERCICIO:

• Resolución de ecuaciones: método de bisección.

Casos en la que la antimagen es el conjunto vacío:

Resolución de una ecuación por bisección:

CONVEXIDAD DE UNA FUNCIÓN

Una función puede ser:

EJEMPLO:

-Una función es convexa hacia arriba en Dominio, intervalo o xo; si la región determinada por su gráfica es convexa.

• Región plana convexa: una región plana se dice convexa cuando el segmento que une 2 puntos cualesquiera de esa región, está contenida en dicha región.

EJERCICIO:

Convexidad de funciones:

Convexa hacia arriba y convexa hacia abajo .

No es convexa hacia arriba ni convexa hacia abajo. 

Proposición:

EJERCICIO:

EJERCICIOS SOBRE DERIVADAS.

DERIVADAS 6.

• Derivadas sucesivas (Derivadas n-ésimas)

Para resolver un ejercicio de una derivada sucesiva hay que emplear el principio de inducción o demostración por inducción:

 EJERCICIO:

DERIVADAS 5.

• Regla de la cadena con 3 funciones

Fórmula:

EJERCICIO:

• Derivada de la potenciación

observación:      

EJERCICIO:

DERIVADAS 4.

• Funciones trigonométricas:

• Funciones inversas:

• Funciones recíprocas:

A partir de la fórmula de la función recíproca podemos demostrar la fórmula del arcsenx:

Recordamos la fórmula:

Demostración: