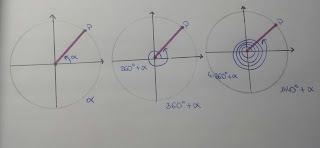
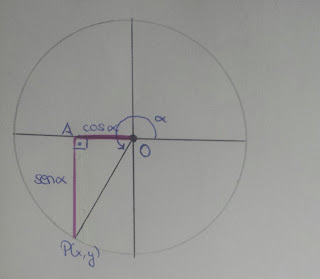
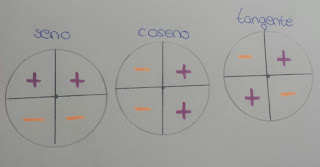
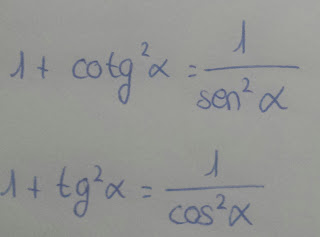EJERCICIO 3 EXAMEN PARA CASA

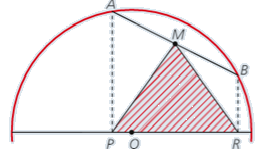
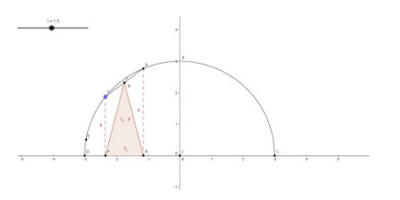
Una barra de longitud constante AB se desliza sobre una semicircunferencia, de modo que sus extremos A y B están siempre sobre la circunferencia. En cada posición de la barra proyectamos los extremos de la misma sobre el diámetro de la semicircunferencia y construimos el triángulo de vértices MPR, siendo M el punto medio de la barra. ¿Cómo evoluciona este triángulo?

A) Elabora una construcción dinámica con GEOGEBRA que permita ver dicha evolución.

B) Demuestra, utilizando el teorema de Tales, que el triángulo MPR es isósceles.

EJERCICIO 2 (examen para casa)

• Se quiere reconstruir la ubicación y las dimensiones de un claustro de forma cuadrada desaparecido y del que se ha encontrado su pozo. Se tienen dudas de la ubicación del pozo en relación al claustro pero se sabe que dicho poco distaba 30,40, 50 m de las esquinas del claustro.

Realizamos un sistema para calcular el lado del cuadrado empleando el teorema del coseno:

EXAMEN PARA CASA TRIGONOMETRÍA

EJERCICIO 1:

Incentro: punto de intersección de las bisectrices de 2 ángulos interiores cualesquiera de dicho triángulo.

Para poder saber que es o no una corona circular debemos calcular el área que se encuentra entre ambas circunferencias.

Para calcular el área total de la figura, primero calculamos el lado c y así obtener el radio del círculo grande y conseguir el área; calculamos el radio del círculo pequeño mediante la tangente de B y de ahí obtener dicho área; restamos ambas áreas y obtenemos el área entre los 2 círculos.
 
No es una corona circular ya que las dos circunferencias no son concéntricas.

Fórmula de Herón

En las expresiones anteriores, es necesario conocer las medidas de alguno de sus lados y de los ángulos; para ello, empleamos la fórmula de Herón.

Expresiones del área de un triángulo

Sabemos que el área de un triángulo es:

A= (b*h)/2

Utilizando la expresión del valor del seno del ángulo A en el triángulo obtenemos:

                                                           sen A= h/b

Llevando el valor de la altura (h) a la fórmula del área de un triángulo:

• El área de un triángulo puede calcularse mediante el producto de un medio por un lado, por otro lado y por el seno del ángulo comprendido entre ambos lados.

Resolución de triángulos cualesquiera:

Resolver un triángulo cualquiera es determinar en él todos sus elementos conocidos.

• Para resolver un triángulo cualquiera, tenemos en cuenta las siguientes relaciones entre sus elementos:

1. La suma de sus ángulos es igual a 180º.
2. El teorema de los senos.
3. El teorema del coseno.

Teorema del coseno.

El teorema del coseno afirma que, en un triángulo cualquiera, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de ellos por el coseno del ángulo que forman.

DEMOSTRACIÓN:

Dado el triángulo: 

Resolvemos:

El teorema del coseno se utiliza en todos aquellos casos en los cuales intervienen triángulos de los que conocemos más lados que ángulos. En los otros casos utilizamos el teorema del seno.

Con el teorema del coseno podemos calcular:

1. Un ángulo de un triángulo del que son conocidos sus tres lados.
2. Un lado del triángulo conocidos los otros dos y el ángulo comprendido entre ellos.

Teorema de los senos.

El teorema de los senos afirma que, en un triángulo cualquiera, los lados son proporcionales a los senos de sus ángulos opuestos.

DEMOSTRACIÓN:

Dado el triángulo:

Tenemos: 

El teorema de los senos se emplea para:

1. Calcular el lado de un triángulo, conociendo su ángulo opuesto, otro lado y su ángulo opuesto.
2. Calcular un ángulo, conociendo su lado opuesto, otro ángulo y su lado opuesto.

Reducción de un ángulo al primer giro y al primer cuadrante.

• Dos ángulos α, k * 360º + α, que difieren en un número entero de vueltas, son equivalentes:

y sus razones trigonométricas coinciden.

• Reducir un ángulo al primer cuadrante es expresar sus razones trigonométricas en función de las razones trigonométricas de un ángulo del primer cuadrante.

Relaciones entre las razones trigonométricas de cualquier ángulo.

Para cualquier ángulo α, las líneas trigonométricas que definen el seno y coseno del ángulo α forman junto con el radio, de longitud uno, un triángulo rectángulo OAP. 

Aplicando el teorema de Pitágoras en este triángulo, tenemos :

Esta igualdad se conoce con el nombre de relación fundamental de la trigonometría.

En la siguiente igualdad aparecen las tres razones trigonométricas más importantes:

Dividiendo en la relación fundamental obtenemos:

Signo de las razones trigonométricas

El signo de las razones trigonométricas seno y coseno, en cada uno de los cuadrantes, viene dado por el signo que en este tengan la ordenada y la abscisa. El signo de la tangente se obtiene por el cociente.

Razones trigonométricas de un ángulo cualquiera:

Las razones trigonométricas de un ángulo cualquiera se definen por la siguiente manera:

• sen α = ordenada de P/ radio = y/r
• cos α = abscisa de P / radio = x/r
• tg α = ordenada de P / abscisa de P = y/x

LÍNEA DEL TIEMPO, LOS FILÓSOFOS MATEMÁTICOS.

1.-  Tales de Mileto   625 aC - 547 aC 
2.-  Anaximandro de Mileto  610 aC - 546 aC 
3.-  Pitágoras de Samos   570 aC - 469 aC 
4.-  Filolao de Tarento   470 aC - 385 aC 
5.-  Eudoxo de Cnido   390 aC – 337 aC 
6.-  Aristarco de Samos   310 aC - 230 aC 
7.-  Eratóstenes de Cirene  276 aC – 194 aC 
8.-  Apolonio de Perga   262 aC - 190 aC 
9.-  Hiparco de Nicea   190 aC - 120 aC 
10.- Menelao de Alejandría  70 dC – 140 dC 
11.- Claudio Ptolomeo de Alejandría 90 dC - 168 dC 

RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS POR TRIGONOMETRÍA

1. La suma de los dos ángulos agudos es igual a 90º: B+C = 90º
2. Teorema de Pitágoras: h^2 = a^2 + b^2
3. Razones trigonométricas seno, coseno y tangente.

Un triángulo rectángulo queda determinado cuando conocemos al menos 2 de sus elementos que no sean 2 ángulos agudos.

Seguimos con trigonometría...

Los ángulos se pueden medir con grados, minutos y segundos pero la mejor forma de medida son los radianes.
Un radián es el ángulo central que abarca un arco que mide un radio (rad).

• Un ángulo completo(360º): mide 2 pi radianes
• El ángulo llano (180º) mide pi radianes
• El ángulo recto (90º) mide pi/2 radianes
• 45º = pi/4 radianes
• 30º = pi/6 radianes
• 60º = 2pi/3 radianes

RAZONES TRIGONOMÉTRICAS DE 30º, 45º Y 60º

TEMA 4: TRIGONOMETRÍA

Y... ¡comenzamos el segundo trimestre!
La trigonometría consiste en el cálculo de lados y ángulos en un triángulo.
Para ello debemos saber las razones trigonométricas de un triángulo:

Con ello podemos calcular el seno, coseno y la tangente:
-El seno de un ángulo es la razón que existe entre el cateto opuesto al ángulo y la hipotenusa:

                                           SENO= CATETO OPUESTO/HIPOTENUSA

-El coseno de un ángulo es la razón que existe entre el cateto adyacente al ángulo y la hipotenusa:

                                                COSENO= CATETO ADYACENTE/ HIPOTENUSA

- La tangente de un ángulo es la razón que existe entre el cateto opuesto al ángulo y el cateto adyacente:
                                    TANGENTE= CATETO OPUESTO/ CATETO ADYACENTE

A partir de estas 3 razones podemos definir otras 3 inversas a ellas:

• Cosecante de un ángulo es la razón que existe entre la hipotenusa y el cateto opuesto:

                                                 COSECANTE= HIPOTENUSA/ CATETO OPUESTO

• Secante de un ángulo es la razón que existe entre la hipotenusa y el cateto adyacente:

                                             SECANTE= HIPOTENUSA/CATETO ADYACENTE

• Cotangente de un ángulo es la razón que existe entre el cateto adyacente y el cateto opuesto:

                                      COTANGENTE=CATETO ADYACENTE/CATETO OPUESTO